LE MODÈLE MATHÉMATIQUE




À L'INTÉRIEUR
La glace s’écoule car c’est un fluide. Le modèle met en équations deux lois fondamentales de la physique. D’une part, la glace est un fluide incompressible, donc un cube de glace se déforme en gardant le même volume et la même masse : c’est la loi de conservation de la masse. D’autre part, la glace est en équilibre, l’accélération est nulle, donc la somme des forces qui s’exercent sur un cube de glace est nulle : c’est la loi de conservation de la quantité de mouvement, ou deuxième loi de Newton.
Il faut aussi une équation pour définir la température à l’intérieur : c’est la loi de conservation de l’énergie, qui prend en compte le flux géothermique et la température de surface. En pratique, on calcule souvent la température séparément, avec un modèle simplifié.
On obtient ainsi un ensemble d’équations, qui s’appellent les équations de Stokes, et qui décrivent des relations entre les variations dans chaque direction de l’espace de la vitesse et de la pression : ce sont des équations aux dérivées partielles.
À LA BASE
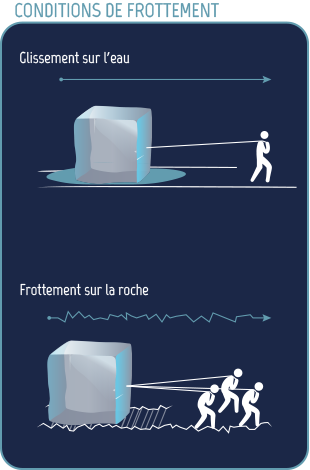
Les conditions de frottement et glissement sont complexes et sont souvent modélisées par une loi de friction (encore une équation avec des dérivées partielles) qui fait intervenir un coefficient de friction propre au glacier étudié. Ce coefficient varie en espace et est très difficile à mesurer.
De plus, l’altitude du socle peut varier. En effet, le socle rocheux s’enfonce très lentement sous le poids de la glace. Il y a une rétroaction entre le bilan de masse de surface, l’écoulement du glacier et l’altitude du socle. Cet enfoncement, appelé isostasie, se produit au bout d’environ 10 000 ans et peut donc être ignoré lorsqu’on étudie l’évolution de l’inlandsis durant un siècle.
EN SURFACE
L’altitude de surface peut augmenter par accumulation ou décroître par ablation. Elle peut aussi varier à cause du mouvement du glacier. L’équation qui traduit l’évolution au cours du temps de l’altitude de surface est un Bilan de Masse de Surface (BMS). L’accumulation et l’ablation sont calculées grâce à un modèle climatique, tandis que le changement dû au mouvement est calculé avec la vitesse du glacier. Le Bilan de Masse de Surface est encore une équation aux dérivées partielles, avec non seulement des variations dans l’espace de l’altitude mais aussi une variation dans le temps.
AU NIVEAU DE LA MER
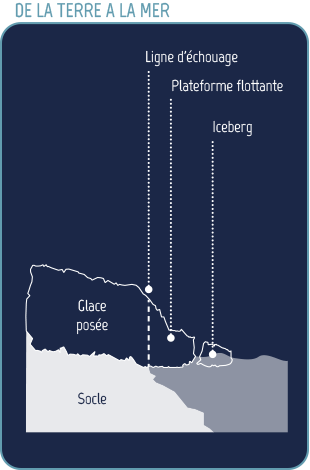
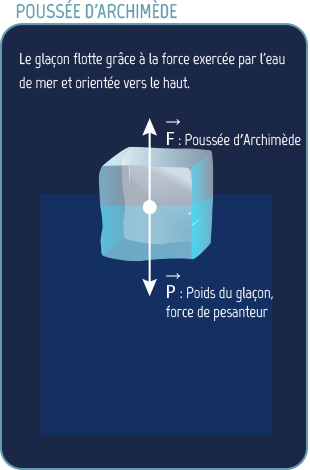
La ligne d’échouage correspond à l’endroit où la calotte polaire se met à flotter sur l’océan. La plate-forme flottante est soumise en plus à la poussée d’Archimède exercée par l’eau. Une équation traduit l’équilibre des forces pour la frontière entre la calotte polaire et l’océan, en tenant compte de la différence des masses volumiques entre la glace et l’eau.
Une équation porte aussi sur les autres frontières de la calotte polaire pour compléter le système.